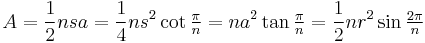Regular polygon

Set of convex regular p-gons
Regular polygons
Edges and vertices	p
Schläfli symbol	{p}
Coxeter–Dynkin diagram
Symmetry group	Dihedral (D_p)
Dual polygon	Self-dual
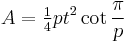Area (with t=edge length)	$A = \tfrac14pt^2 \cot \frac{\pi}{p}$
Internal angle	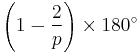$\left(1-\frac{2}{p}\right)\times 180^\circ$
Internal angle sum	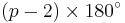$\left(p-2\right)\times 180^\circ$
Properties	convex, cyclic, equilateral, isogonal, isotoxal

A regular polygon is a polygon which is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star.

1 General properties
- 1.1 Symmetry
2 Regular convex polygons
3 Regular star polygons
4 Duality of regular polygons
5 Regular polygons as faces of polyhedra
6 See also
7 Notes
8 References
9 External links

General properties

These properties apply to all regular polygons (both convex and a star).

A regular n-sided polygon has rotational symmetry of order n.

All vertices of a regular polygon lie on a common circle (the circumscribed circle), i.e., they are concyclic points.

Together with the property of equal-length sides, this implies that every regular polygon also has an inscribed circle or incircle.

A regular n-sided polygon can be constructed with compass and straightedge if and only if the odd prime factors of n are distinct Fermat primes. See constructible polygon.

Symmetry

The symmetry group of an n-sided regular polygon is dihedral group D_n (of order 2n): D₂, D₃, D₄,... It consists of the rotations in C_n, together with reflection symmetry in n axes that pass through the center. If n is even then half of these axes pass through two opposite vertices, and the other half through the midpoint of opposite sides. If n is odd then all axes pass through a vertex and the midpoint of the opposite side.

Regular convex polygons

All regular simple polygons (a simple polygon is one which does not intersect itself anywhere) are convex. Those having the same number of sides are also similar.

An n-sided convex regular polygon is denoted by its Schläfli symbol {n}.

Henagon or monogon {1}: degenerate in ordinary space (Most authorities do not regard the monogon as a true polygon, partly because of this, and also because the formulae below do not work, and its structure is not that of any abstract polygon).
Digon {2}: a "double line segment": degenerate in ordinary space (Some authorities do not regard the digon as a true polygon because of this).
Equilateral triangle {3}
Square (regular tetragon or quadrilateral) {4}
Regular pentagon {5}
Regular hexagon {6}
Regular heptagon {7}
Regular octagon {8}
Regular nonagon or enneagon {9}
Regular decagon {10}
Regular hendecagon {11}
Regular dodecagon {12}
Regular tridecagon (or triskaidecagon) {13}
Regular tetradecagon (or tetrakaidecagon) {14}
Regular pentadecagon (or pentakaidecagon) {15}
Regular hexadecagon (or hexakaidecagon) {16}
Regular heptadecagon (or heptakaidecagon) {17}
Regular octadecagon (or octakaidecagon) {18}
Regular enneadecagon (or enneakaidecagon or nonadecagon) {19}
Regular icosagon {20}
Regular triacontagon or tricontagon {30}
Regular tetracontagon {40}
Regular pentacontagon {50}
Regular hexacontagon {60}
Regular heptacontagon {70}
Regular octacontagon {80}
Regular enneacontagon {90} (or nonacontagon)
Regular hectogon {100}^[1]

In certain contexts all the polygons considered will be regular. In such circumstances it is customary to drop the prefix regular. For instance all the faces of uniform polyhedra must be regular and the faces will be described simply as triangle, square, pentagon, etc.

Angles

For a regular convex n-gon, each interior angle has a measure of:

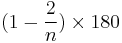$(1-\frac{2}{n})\times 180$ (or equally of 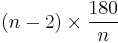$(n-2)\times \frac{180}{n}$ ) degrees,

or 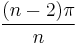$\frac{(n-2)\pi}{n}$ radians,

or 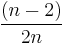$\frac{(n-2)}{2n}$ full turns,

and each exterior angle (supplementary to the interior angle) has a measure of 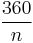$\frac{360}{n}$ degrees, with the sum of the exterior angles equal to 360 degrees or 2π radians or one full turn.

Diagonals

For 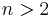$n > 2$ the number of diagonals is 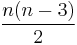$\frac{n (n-3)}{2}$ , i.e., 0, 2, 5, 9, ... They divide the polygon into 1, 4, 11, 24, ... pieces.

Radius

The radius from the centre of a regular polygon to one of the vertices is related to the side length, s or apothem, a:

$r=\frac{s} {2 \sin{ \frac{\pi}{n} }} = \frac{a} {\cos{ \frac{\pi}{n} }}$

Area

Relgular polygon with n = 5: pentagon with side s, apothem a, and circumradius r

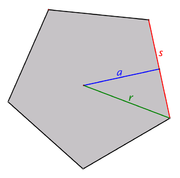
The area A of a convex regular n-sided polygon having side s, apothem a, and circumradius r is given by ^[2]

$A= \frac{1}{2}nsa = \frac{1}{4}ns^2\cot{\tfrac{\pi}{n}} = na^2\tan{\tfrac{\pi}{n}} = \frac{1}{2}nr^2\sin{\tfrac{2\pi}{n}}$

For regular polygons with side s=1 this produces the following table:

Sides	Name	Exact area	Approximate area
n	regular n-gon	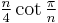$\tfrac{n}{4}\cot{\tfrac{\pi}{n}}$
3	equilateral triangle	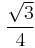$\frac{\sqrt{3}}{4}$	0.433012702
4	square	1
5	regular pentagon	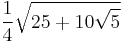$\frac {1}{4} \sqrt{25+10\sqrt{5}}$	1.720477401
6	regular hexagon	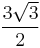$\frac{3 \sqrt{3}}{2}$	2.598076211
7	regular heptagon		3.633912444
8	regular octagon	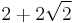$2 + 2 \sqrt{2}$	4.828427125
9	regular nonagon		6.181824194
10	regular decagon	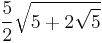$\frac{5}{2} \sqrt{5+2\sqrt{5}}$	7.694208843
11	regular hendecagon		9.365639907
12	regular dodecagon	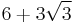$6+3\sqrt{3}$	11.19615242
13	regular triskaidecagon		13.18576833
14	regular tetradecagon		15.33450194
15	regular pentadecagon		17.64236291
16	regular hexadecagon		20.10935797
17	regular heptadecagon		22.73549190
18	regular octadecagon		25.52076819
19	regular enneadecagon		28.46518943
20	regular icosagon		31.56875757
100	regular hectagon		795.5128988
1000	regular chiliagon		79577.20975
10000	regular myriagon		7957746.893
1,000,000	regular megagon		79,577,471,545.685

The amounts that the areas are less than those of circles with the same perimeter, are (rounded) equal to 0.28 for n=3, 0.27 for 3<n<7, 0.26 (rounded down) for n>7, reducing as n increases to 0.262 for n>15 and to 0.2618 for all n>58.

Regular star polygons

A pentagram {5/2}

A non-convex regular polygon is a regular star polygon. The most common example is the pentagram, which has the same vertices as a pentagon, but connects alternating vertices.

For an n-sided star polygon, the Schläfli symbol is modified to indicate the density or 'starriness' m of the polygon, as {n/m}. If m is 2, for example, then every second point is joined. If m is 3, then every third point is joined. The boundary of the polygon winds around the centre m times.

The (non-degenerate) regular stars of up to 12 sides are:

Pentagram - {5/2}
Heptagram - {7/2} and {7/3}
Octagram - {8/3}
Enneagram - {9/2} and {9/4}
Decagram - {10/3}
Hendecagram - {11/2}, {11/3}, {11/4} and {11/5}
Dodecagram - {12/5}

m and n must be co-prime, or the figure will degenerate.

The degenerate regular stars of up to 12 sides are:

Hexagram - {6/2}
Octagram - {8/2}
Enneagram - {9/3}
Decagram - {10/2} and {10/4}
Dodecagram - {12/2}, {12/3} and {12/4}

Depending on the precise derivation of the Schläfli symbol, opinions differ as to the nature of the degenerate figure. For example {6/2} may be treated in either of two ways:

For much of the 20th century (see for example Coxeter (1948)), we have commonly taken the /2 to indicate joining each vertex of a convex {6} to its near neighbours two steps away, to obtain the regular compound of two triangles, or hexagram.
Many modern geometers, such as Grünbaum (2003), regard this as incorrect. They take the /2 to indicate moving two places around the {6} at each step, obtaining a "double-wound" triangle that has two vertices superimposed at each corner point and two edges along each line segment. Not only does this fit in better with modern theories of abstract polytopes, but it also more closely copies the way in which Poinsot (1809) created his star polygons - by taking a single length of wire and bending it at successive points through the same angle until the figure closed.

Duality of regular polygons

All regular polygons are self-dual to congruency, and for odd n they are self-dual to identity.

In addition the regular star figures (compounds), being composed of regular polygons, are also self-dual.

Regular polygons as faces of polyhedra

A uniform polyhedron has regular polygons as faces, such that for every two vertices there is an isometry mapping one into the other (just as there is for a regular polygon).

A quasiregular polyhedron is a uniform polyhedron which has just two kinds of face alternating around each vertex.

A regular polyhedron is a uniform polyhedron which has just one kind of face.

The remaining (non-uniform) convex polyhedra with regular faces are known as the Johnson solids.

A polyhedron having regular triangles as faces is called a deltahedron.

Notes

References

Coxeter, H. S. M. (1948). Regular Polytopes. Methuen and Co.
Grünbaum, B.; Are your polyhedra the same as my polyhedra?, Discrete and comput. geom: the Goodman-Pollack festschrift, Ed. Aronov et al., Springer (2003), pp. 461–488.
Poinsot, L.; Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9 (1810), pp. 16–48.

External links

Weisstein, Eric W., "Regular polygon" from MathWorld.
Regular Polygon description With interactive animation
Incircle of a Regular Polygon With interactive animation
Area of a Regular Polygon Three different formulae, with interactive animation
Renaissance artists' constructions of regular polygons at Convergence

Polygons

Listed by number of sides

1–10 sides	Henagon (Monogon) · Digon · Triangle (Trigon) · Quadrilateral (Tetragon) · Pentagon · Hexagon · Heptagon · Octagon · Nonagon (Enneagon) · Decagon

11–20 sides	Hendecagon · Dodecagon · Triskaidecagon · Tetradecagon · Pentadecagon · Hexadecagon · Heptadecagon · Octadecagon · Nonadecagon (Enneadecagon) · Icosagon

Others	Apeirogon

Star polygons	Pentagram · Hexagram · Heptagram · Octagram · Enneagram · Decagram · Hendecagram · Dodecagram